In the realm of medical research and statistical analysis, the P-value stands as one of the most frequently cited yet often misunderstood concepts. In practice, it (incorrectly) is reduced by some clinicians as a binary classifier of a ‘significant’ or ‘not significant’ results. In reality, it’s a probability value that tells us how likely it is to observe the data, or something more extreme, if the null hypothesis is true. This explanation is jargony and can be confusing, so lets make it simple and start by first exploring what a P-value is not.
What a P-value is NOT
1. Not the Probability of the Hypothesis Being True: A common misconception is that the P-value indicates the probability of the alternative hypothesis being true (i.e. that there is a difference between groups). This is incorrect. It is actually the probability that the results were obtained if the hypothesis that there was no difference between groups was true (aka the null hypothesis). Importantly, these two statements are not the inverse of each other.
For example, a P-value of 0.03 does not mean there is a 97% chance that there is a difference between groups.
2. Not About the Probability of Random Chance: While it’s related to the idea of ‘chance,’ the P-value is not a measure of the probability that the observed results are due to chance alone.
For example, a P-value of 0.03 does NOT mean that there is a 3% chance that the results were obtained by chance alone.
3. Not a Measure of Effect Size: The P-value does not provide information on the magnitude of an effect. A small P-value does not mean a clinically significant difference, just as a large P-value doesn’t imply clinical insignificance.
For example, a drug could reduce cholesterol by 0.05mg/dl with a p-value of <0.0001 (statistically significant) but this could be clinically insignificant with respect to reducing the risk for cardiovascular events.
4. Not a Benchmark for Truth: A P-value alone cannot prove or disprove a theory. It’s a tool for assessing evidence, not a definitive statement of fact.
For example, the statement “well the P-value was greater than 0.05 so we shouldn’t use drug X” is incorrect.
The True Meaning of a P-value
The true definition of a P-value is the probability of observing the data, or something more extreme, if there truly was no difference between groups (e.g. the null hypothesis was true). In simpler terms, it answers the question, “If there were really no difference between groups, how likely is it that we would observe these results?”
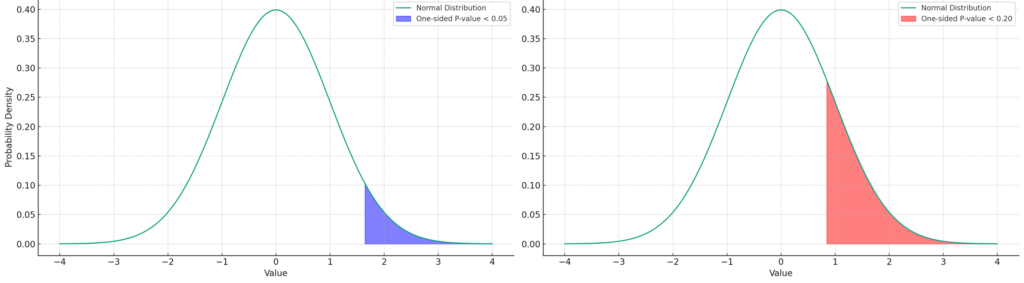
Figure 1. If there is no difference between groups (null hypothesis true), the shaded area shows the magnitude of difference between groups to reject the null hypothesis at P<0.05 (purple) and P<0.20 (red).
Difference between P-values and Confidence Intervals
Comparing P-values to confidence intervals is like looking at two sides of the same coin. Both are methods of statistical inference that convey similar information.
P-values: Offer a probability measure that the results are obtained if the null hypothesis was true.
Confidence Intervals: Provide a range of values within which the true effect size is likely to fall. For example, 95% confidence is a range that you can be 95% certain contains the true population mean. When interpreting confidence intervals, if they cross the line of no effect, we reject the null hypothesis.
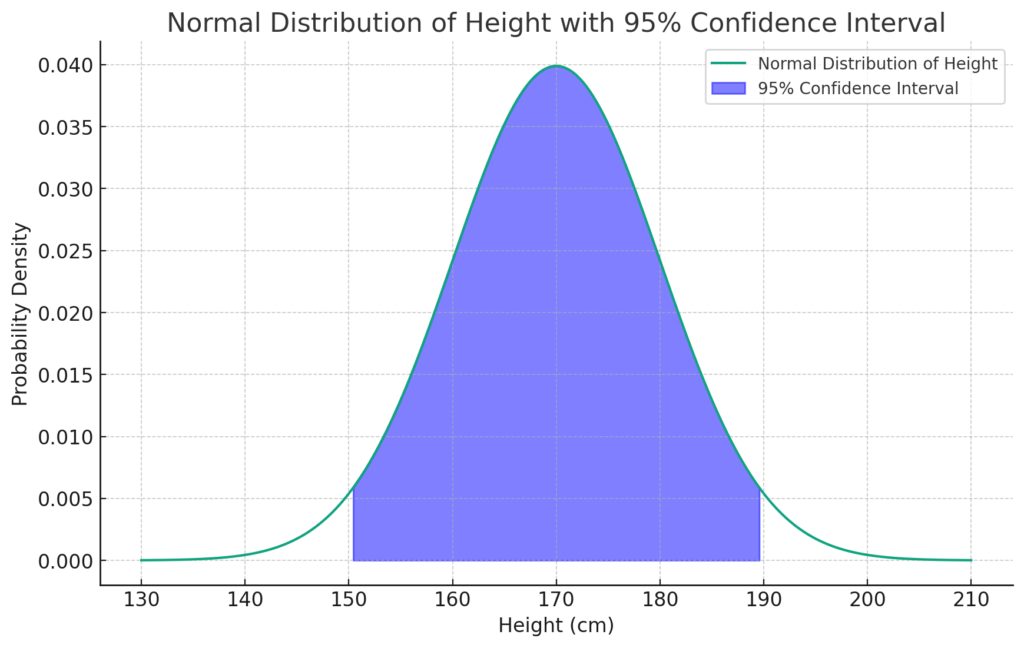
Figure 2. In this example of heights, we can see that the 95% confidence interval is the range that there is a 95% chance the true population mean lies within.
How to use P-values in practice
Understanding P-values are crucial for clinicians and researchers as we navigate the complex world of research and evidence-based medicine, and strive to design high quality research. It’s important to recognize what P-values can and cannot tell us about our data and research findings. Most importantly, blind reliance on P-values as the arbitrator of truth (e.g. P-value of <0.05 = true difference) is not appropriate, and may lead to misinterpretation of scientific research. In recent years, there has been a slow movement away from P-values towards Bayesian interpretation of trial results – but until that becomes the norm, we will continue to struggle with appropriate application of P-values to clinical practice.
For more reading about P-values, I recommend checking out this video by Steven Bradburn simply describing P-values.